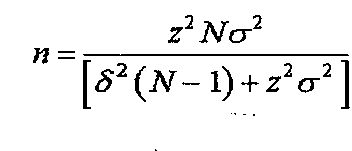
Calcolo della numerosità ottimale del campione
Qui potrai calcolare
il Campionamento esaustivo senza reimmissione;
il Campionamento bernoulliano con reimmissione;
il Campionamento esaustivo senza reimbussolamento;
il Campione bernoulliano con reimbussolamento.
Ecco un esempio di Campionamento esaustivo senza reimmissione
Questa é la formula che permette il calcolo della numerosità ottimale del campione
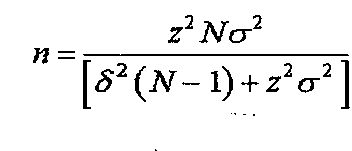
Legenda
N è la numerosità della popolazione
Sigma quadro è la varianza della popolazione
Delta è l’errore assoluto ammesso per la stima del parametro
Z costante (corrispondente al valore della variabile casuale normale standardizzata)
che dipende dal livello di fiducia desiderato per la stima.
Ecco un esempio di Campionamento bernoulliano con reimmissione
Questa é la formula che permette il calcolo della numerosità ottimale del campione
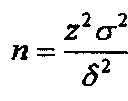
Legenda
Sigma quadro è la varianza della popolazione
Delta è l’errore assoluto ammesso per la stima del parametro
Z costante (corrispondente al valore della variabile casuale normale standardizzata)
che dipende dal livello di fiducia desiderato per la stima.
N.B.: se la popolazione si può considerare infinita (N molto grande), la numerosità della popolazione non influenza la numerosità campionaria ottimale.
Ecco un esempio di Campionamento esaustivo senza reimbussolamento
Questa é la formula che permette il calcolo della numerosità ottimale del campione
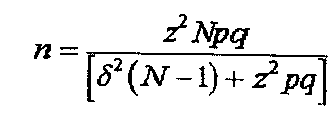
Legenda
N è la numerosità
della popolazione
z è il valore della
variabile casuale normale standardizzata per il livello di fiducia
desiderato
Delta è l’errore
ammesso per la stima del parametro (es 0,03)
P è la proporzione
da stimare nella popolazione da studiare; se non si ha un’idea del valore che
può assumere conviene mettersi nella situazione più svantaggiosa, ovvero p =
0,5, per il quale il valore di n diventa elevato
Q= 1-P
Ecco un esempio di Campionamento bernoulliano con reimbussolamento
Questa é la formula che permette il calcolo della numerosità ottimale del campione

Delta è l’errore
ammesso per la stima del parametro (es 0,03)
P è la proporzione da
stimare nella popolazione da studiare; se non si ha un’idea del valore che può
assumere conviene mettersi nella situazione più svantaggiosa, ovvero p = 0,5,
per il quale il valore di n
diventa elevato
Per maggiori informazioni vedi anche il Corso di Metodologia della Ricerca Sociale (R. GRIMALDI)
Campionamento esaustivo senza reimmissione
Campionamento bernoulliano con reimmissione
Campionamento esaustivo senza reimbussolamento
Campione bernoulliano con reimbussolamento